Purpose
The purpose of this section is to provide the reader with grounding in the fundamental philosophical principles of data mining as a technical practice. The reader is then introduced to the wide array of practical applications that rely on data mining technology. The issue of computational complexity is addressed in brief.
Goals
After you have read this section, you will be able to define data mining from both philosophical and operational perspectives, and enumerate the analytic functions data mining performs. You will know the different types of data that arise in practice. You will understand the basics of computational complexity theory. Most importantly, you will understand the difference between data and information.
1. Introduction
Our study of data mining begins with two semi-formal definitions:
Definition 1. Data mining is the principled detection, characterization, and exploitation of actionable patterns in data. Table 1 explains what is meant by each of these components.
===============
Table 1 Definitive Data Mining Attributes
Attribute | Connotations
Principled Rational, empirical, objective, repeatable
Detection Sensing and locating
Characterization Consistent, efficient, tractable symbolic representation that does not alter information content
Exploitation Decision making that facilitates action
Actionable Pattern Conveys information that supports decision making
================
Taking this view of what data mining is we can formulate a functional definition that tells us what individuals engaged in data mining do.
Definition 2. Data Mining is the application of the scientific method to data to obtain useful information. The heart of the scientific approach to problem-solving is rational hypothesis testing guided by empirical experimentation.
What we today call science today was referred to as natural philosophy in the 15th century. The Aristotelian approach to understanding the world was to catalog and organize more-or-less passive acts of observation into taxonomies. This method began to fall out of favor in the physical sciences in the 15th century, and was dead by the 17th century. However, because of the greater difficulty of observing the processes underlying biology and behavior, the life sciences continued to rely on this approach until well into the 19th century. This is why the life sciences of the 1800s are replete with taxonomies, detailed naming conventions, and perceived lines of descent, which are more a matter of organizing observations than principled experimentation and model revision.
Applying the scientific method today, we expect to engage in a sequence of planned steps:
1. Formulate hypotheses (often in the form of a question)
2. Devise experiments
3. Collect data
4. Interpret data to evaluate hypotheses
5. Revise hypotheses based upon experimental results
This sequence amounts to one cycle of an iterative approach to acquiring knowledge. In light of our functional definition of data mining, this sequence can be thought of as an over-arching data mining methodology that will be described in detail in Section 3.
2. A Brief Philosophical Discussion
Somewhere in every data mining effort, you will encounter at least one computation ally intractable problem; it is unavoidable. This has technical and procedural implications, but it also has philosophical implications. In particular, since there are by definition no perfect techniques for intractable problems, different people will handle them in different ways; no one can say definitively that one way is necessarily wrong and another right. This makes data mining something of an art, and leaves room for the operation of both practical experience and creative experimentation. It also implies that the data mining philosophy to which you look when science falls short can mean the difference between success and failure. Let's talk a bit about developing such a data mining philosophy.
As noted above, data mining can be thought of as the application of the scientific method to data. We perform data collection (sampling), formulate hypotheses (e.g., visualization, cluster analysis, feature selection), conduct experiments (e.g., construct and test classifiers), refine hypotheses (spiral methodology), and ultimately build theories (field applications). This is a process that can be reviewed and replicated. In the real world, the resulting theory will either succeed or fail.
Many of the disciplines that apply to empirical scientific work also apply to the practice of data mining: assumptions must be made explicit; the design of principled experiments capable of falsifying our hypotheses is essential; the integrity of the evidence, process, and results must be meticulously maintained and documented; out comes must be repeatable; and so on. Unless these disciplines are maintained, nothing of certain value can result. Of particular importance is the ability to reproduce results.
In the data mining world, these disciplines involve careful configuration management of the system environment, data, applications, and documentation. There are no effective substitutes for these.
One of the most difficult mental disciplines to maintain during data mining work is reservation of judgment. In any field involving hypothesis and experimentation, preliminary results can be both surprising and exhilarating. Finding the smoking gun in a forensic study, for example, is hitting pay-dirt of the highest quality, and it is hard not to get a little excited if you smell gunpowder.
However, this excitement cannot be allowed to short-circuit the analytic pro cess. More than once I have seen exuberant young analysts charging down the hall to announce an amazing discovery after only a few hours' work with a data set; but I don't recall any of those instant discoveries holding up under careful review. I can think of three times when I have myself jumped the gun in this way. On one occasion, eagerness to provide a rapid response led me to prematurely turn over results to a major customer, who then provided them (without review) to their major customer.
Unfortunately, there was an unnoticed but significant f law in the analysis that invalidated most of the reported results. That is a trail of culpability you don't want leading back to your office door.
3. The Most Important Attribute of the Successful Data Miner: Integrity
Integrity is variously understood, so we list the principal characteristics data miners must have.
• Moral courage. Data miners have lots of opportunities to deliver unpleasant news. Sometimes they have to inform an enterprise that the data it has collected and stored at great expense does not contain the type or amount of information expected.
Further, it is an unfortunate fact that the default assessment for data mining efforts in most situations is "failure." There can be tremendous pressure to pro duce a certain result, accuracy level, conclusion, etc., and if you don't: Failure.
Pointing out that the data do not support the desired application, are of low quality (precision/accuracy), and do not contain sufficient samples to cover the problem space will sound like excuses, and will not always redeem you.
• Commitment to enterprise success. If you want the enterprise you are assisting to be successful, you will be honest with them; will labor to communicate information in terms they can understand; and will not put your personal success ahead of the truth.
• Honesty in evaluation of data and information. Individuals that demonstrate this characteristic are willing to let the data speak for itself. They will resist the temptation to read into the data that which wasn't mined from the data.
• Meticulous planning, execution, and documentation. A successful data miner will be meticulous in planning, carrying out, and documenting the mining process. They will not jump to conclusions; will enforce the prerequisites of a process before beginning; will check and recheck major results; and will carefully validate all results before reporting them. Excellent data miners create documentation of sufficient quality and detail that their results can be reproduced by others.
4. What Does Data Mining Do?
The particulars of practical data mining "best practice" will be addressed later in great detail, but we jump-start the treatment with some bulleted lists summarizing the functions that data mining provides.
Data mining uses a combination of empirical and theoretical principles to connect structure to meaning by
• Selecting and conditioning relevant data
• Identifying, characterizing, and classifying latent patterns
• Presenting useful representations and interpretations to users
Data mining attempts to answer these questions
• What patterns are in the information?
• What are the characteristics of these patterns?
• Can meaning be ascribed to these patterns and/or their changes?
• Can these patterns be presented to users in a way that will facilitate their assessment, understanding, and exploitation?
• Can a machine learn these patterns and their relevant interpretations?
Data mining helps the user interact productively with the data
• Planning helps the user achieve and maintain situational awareness of vast, dynamic, ambiguous/incomplete, disparate, multi-source data.
• Knowledge leverages users' domain knowledge by creating functionality based upon an understanding of data creation, collection, and exploitation.
• Expressiveness produces outputs of adjustable complexity delivered in terms meaningful to the user.
• Pedigree builds integrated metrics into every function, because every recommendation has to have supporting evidence and an assessment of certainty.
• Change uses future-proof architectures and adaptive algorithms that anticipate many users addressing many missions.
Data mining enables the user to get their head around the problem space
Decision
Support is all about ...
• Enabling users to group information in familiar ways
• Controlling HMI complexity by layering results (e.g., drill-down)
• Supporting user's changing priorities (goals, capabilities)
• Allowing intuition to be triggered ("I've seen this before")
• Preserving and automating perishable institutional knowledge
• Providing objective, repeatable metrics (e.g., confidence factors)
• Fusing and simplifying results (e.g., annotate multisource visuals)
• Automating alerts on important results ("It's happening again")
• Detecting emerging behaviors before they consummate (look)
• Delivering value (timely, relevant, and accurate results)
...helping users make the best choices.
Some general application areas for data mining technology
• Automating pattern detection to characterize complex, distributed signatures that are worth human attention and recognize those that are not
• Associating events that go together but are difficult for humans to correlate
• Characterizing interesting processes not just facts or simple events
• Detecting actionable anomalies and explaining what makes them different and interesting
• Describing contexts from multiple perspectives with numbers, text and graphics
• Accurate identification and classification-add value to raw data by tagging and annotation (e.g., automatic target detection)
Anomaly, normalcy, and fusion-characterize, quantify, and assess normalcy of patterns and trends (e.g., network intrusion detection)
• Emerging patterns and evidence evaluation-capturing institutional knowledge of how events arise and alerting users when they begin to emerge
• Behavior association-detection of actions that are distributed in time and space but synchronized by a common objective: connecting the dots
• Signature detection and association-detection and characterization of multivariate signals, symbols, and emissions
• Concept tagging-ontological reasoning about abstract relationships to tag and annotate media of all types (e.g., document geo-tagging)
• Software agents assisting analysts-small footprint, fire-and-forget apps that facilitate search, collaboration, etc.
• Help the user focus via unobtrusive automation
Off-load burdensome labor (perform intelligent searches, smart winnowing)
Post smart triggers or tripwires to data stream (anomaly detection)
Help with workflow and triage (sort my in-basket)
• Automate aspects of classification and detection
Determine which sets of data hold the most information for a task
Support construction of ad hoc on-the-fly classifiers
Provide automated constructs for merging decision engines (multi-level fusion)
Detect and characterize domain drift (the rules of the game are changing)
Provide functionality to make best estimate of missing data
• Extract, characterize and employ knowledge
Rule induction from data and signatures development from data
Implement non-monotonic reasoning for decision support
High-dimensional visualization
Embed decision explanation capability in analytic applications
• Capture, automate and institutionalize best practices
Make proven enterprise analytic processes available to all
Capture rare, perishable human knowledge and distribute it everywhere
Generate signature-ready prose reports
Capture and characterize the analytic process to anticipate user needs
5. What Do We Mean By Data?
Data is the wrapper that carries information. It can look like just about anything: images, movies, recorded sounds, light from stars, the text in this guide, the swirls that form your fingerprints, your hair color, age, income, height, weight, credit score, a list of your likes and dislikes, the chemical formula for the gasoline in your car, the number of miles you drove last year, your cat's body temperature as a function of time, the order of the nucleotides in the third codon of your mitochondrial DNA, a street map of Liberal Kansas, the distribution of IQ scores in Braman Oklahoma, the fat content of smoked sausage, a spreadsheet of your household expenses, a coded message, a computer virus, the pattern of fibers in your living room carpet, the pattern of purchases at a grocery store, the pattern of capillaries in your retina, election results, etc. In fact: A datum (singular) is any symbolic representation of any attribute of any given thing.
More than one datum constitutes data (plural).
5.1 Nominal Data vs. Numeric Data
Data come in two fundamental forms-nominal and numeric. Fabulously intricate hierarchical structures and relational schemes can be fashioned from these two forms.
This is an important distinction, because nominal and numeric data encode information in different ways. Therefore, they are interpreted in different ways, exhibit patterns in different ways, and must be mined in different ways. In fact, there are many data mining tools that only work with numeric data, and many that only work with nominal data. There are only few (but there are some) that work with both.
Data are said to be nominal when they are represented by a name. The names of people, places, and things are all nominal designations. Virtually all text data is nominal. But data like Zip codes, phone numbers, addresses, social security numbers, etc. are also nominal. This is because they are aliases for things: your postal zone, the den that contains your phone, your house, and you. The point is the information in these data has nothing to do with the numeric values of their symbols; any other unique string of numbers could have been used.
Data are said to be numeric when the information they contain is conveyed by the numeric value of their symbol string. Bank balances, altitudes, temperatures, and ages all hold their information in the value of the number string that represents them. A different number string would not do.
Given that nominal data can be represented using numeric characters, how can you tell the difference between nominal and numeric data? There is a simple test: If the average of a set of data is meaningful, they are numeric.
Phone numbers are nominal, because averaging the phone numbers of a group of people doesn't produce a meaningful result. The same is true of zip codes, addresses, and Social Security numbers. But averaging incomes, ages, and weights gives symbols whose values carry information about the group; they are numeric data.
5.2 Discrete Data vs. Continuous Data
Numeric data come in two forms-discrete and continuous. We can't get too technical here, because formal mathematical definitions of these concepts are deep. For the purposes of data mining, it is sufficient to say that a set of data is continuous when, given two values in the set, you can always find another value in the set between them.
Intuitively, this implies there is a linear ordering, and there aren't gaps or holes in the range of possible values. In theory, it also implies that continuous data can assume infinitely many different values.
A set of data is discrete if it is not continuous. The usual scenario is a finite set of values or symbols. For example, the readings of a thermometer constitute continuous data, because (in theory), any temperature within a reasonable range could actually occur. Time is usually assumed to be continuous in this sense, as is distance; therefore sizes, distances, and durations are all continuous data.
On the other hand, when the possible data values can be placed in a list, they are discrete: hair color, gender, quantum states (depending upon whom you ask), head count for a business, the positive whole numbers (an infinite set) etc., are all discrete.
A very important difference between discrete and continuous data for data mining applications is the matter of error. Continuous data can presumably have any amount of error, from very small to very large, and al l values in between. Discrete data are either completely right or completely wrong.
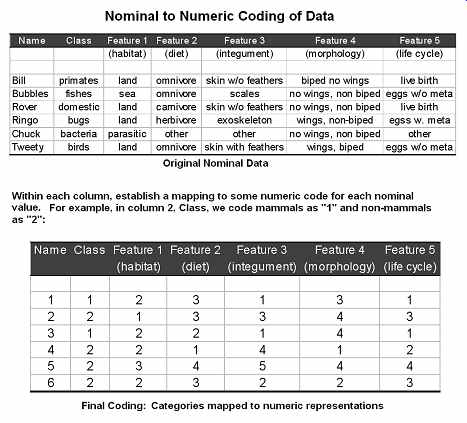
FIG. 1 Nominal to numeric coding of data.
5.3 Coding and Quantization as Inverse Processes
Data can be represented in different ways. Sometimes it is necessary to translate data from one representational scheme to another. In applications this often means converting numeric data to nominal data (quantization), and nominal data to numeric data (coding).
Quantization usually leads to loss of precision, so it is not a perfectly reversible pro cess. Coding usually leads to an increase in precision, and is usually reversible.
There are many ways these conversions can be done, and some application-dependent decisions that must be made. Examples of these decisions might include choosing the level of numeric precision for coding, or determining the number of restoration values for quantization. The most intuitive explanation of these inverse processes is pictorial. Notice that the numeric coding (FIG. 1) is performed in stages. No information is lost; its only purpose was to make the nominal feature attributes numeric.
However, quantization (FIG. 2) usually reduces the precision of the data, and is rarely reversible.
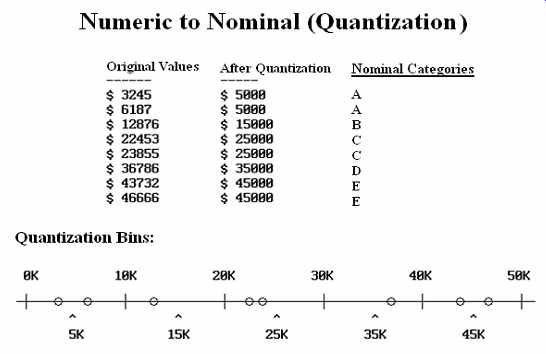
FIG. 2 Numeric to nominal quantization.
5.4 A Crucial Distinction: Data and Information Are Not the Same Thing
Data and information are entirely different things. Data is a formalism, a wrapper, by which information is given observable form. Data and information stand in relation to one another much as do the body and the mind. In similar fashion, it is only data that are directly accessible to an observer. Inferring information from data requires an act of interpretation which always involves a combination of contextual constraints and rules of inference.
In computing systems, the problem "context" and "heuristics" are represented using a structure called a domain ontology. As the term suggests, each problem space has its own constraints, facts, assumptions, rules of thumb, and these are variously represented and applied.
The standard mining analogy is helpful here. Data mining is similar in some ways to mining for precious metals:
• Silver mining. Prospectors survey a region and select an area they think might have ore, the rough product that is refined to obtain metal. They apply tools to estimate the ore content of their samples and if it is high enough, the ore is refined to obtain purified silver.
• Data mining. Data miners survey a problem space and select sources they think might contain salient patterns, the rough product that is refined to obtain information. They apply tools to assess the information content of their sample and if it is high enough, the data are processed to infer latent information.
However, there is a very important way in which data mining is not like silver mining. Chunks of silver ore actually contain particular silver atoms. When a chunk of ore is moved, its silver goes with it. Extending this part of the silver mining analogy to data mining will get us into trouble. The silver mining analogy fails because of the fundamental difference between data and information.
The simplest scenario demonstrating this difference involves their different relation to context. When I remove letters from a word, they retain their identity as letters, as do the letters left behind. But the information conveyed by the letters removed and by the letters left behind has very likely been altered, destroyed, or even negated.
Another example is found in the dependence on how the information is encoded. I convey exactly the same message when I say "How are you?" that I convey when I say "Wie gehts?," yet the data are completely different. Computer scientists use the terms syntax and semantics to distinguish between representation and meaning, respectively.
It is extremely dangerous for the data miner to fall into the habit of regarding particular pieces of information as being attached to particular pieces of data in the same way that metal atoms are bound to ore. Consider a more sophisticated, but subtle example:
A Morse code operator sends a message consisting of alternating, evenly spaced dots and dashes (FIG. 3):

FIG. 3 Non-informative pattern.
This is clearly a pattern but other than manifesting its own existence, this pattern conveys no information. Information Theory tells that us such a pattern is devoid of information by pointing out that after we've listened to this pattern for a while, we can perfectly predict which symbol will arrive next. Such a pattern, by virtue of its complete predictability is not informative: a message that tells me what I already know tells me nothing. This important notion can be quantified in the Shannon Entropy (see glossary). However, if the transmitted tones are varied or modulated, the situation is quite different (FIG. 4):
This example makes is quite clear that information does not reside within the dots and dashes themselves; rather, it arises from an interpretation of their inter-relation ships. In Morse code, this is their order and duration relative to each other. Notice that by removing the first dash from
= - - -, the last two dashes now mean M = - -, even though the dashes have not changed. This context sensitivity is a wonderful thing, but it causes data mining disaster if ignored.
A final illustration called the Parity Problem convincingly establishes the distinct nature of data and information in a data mining context.
5.5 The Parity Problem
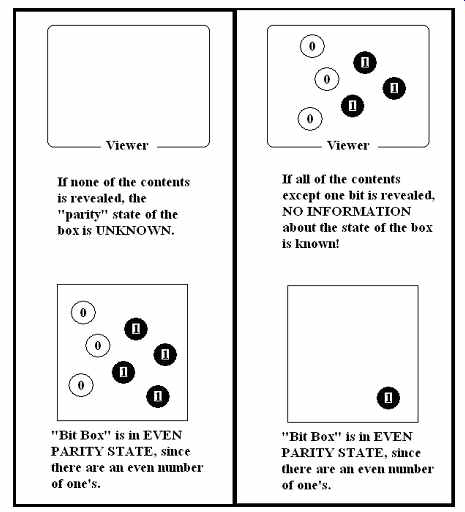
Let's do a thought experiment (FIG. 5). I have two marbles in my hand, one white and one black. I show them to you and ask this question: Is the number of black marbles even, or is it odd?
Naturally you respond odd, since one is an odd number. If both of the marbles had been black, the correct answer would have been even, since 2 is an even number; if I had been holding two white marbles, again the correct answer would have been even, since 0 is an even number.
This is called the Parity Two problem. If there are N marbles, some white (possibly none) and some black (possibly none), the question of whether there are an odd number of black marbles is called the Parity-N Problem, or just the Parity Problem.
This problem is important in computer science, information theory, coding theory, and related areas.
Of course, when researchers talk about the parity problem, they don't use marbles, they use zeros and ones (binary digits = bits). For example, I can store a data file on disc and then ask whether the file has an odd or even number of ones; the answer is the parity of the file.
This idea can also be used to detect data transmission errors: if I want to send you 100 bits of data, I could actually send you 101, with the extra bit set to a one or zero such that the whole set has a particular parity that you and I have agreed upon in advance. If you get a message from me and it doesn't have the expected parity, you know the message has an odd number of bit errors and must be resent.

FIG. 4 Informative modulation pattern.
5.6 Five Riddles about Information
Suppose I have two lab assistants named Al and Bob, and two data bits. I show only the first one to Al, and only the second one to Bob. If I ask Al what the parity of the original pair of bits is, what will he say? And if I ask Bob what the parity of the original pair of bits is, what will he say? Neither one can say what the parity of the original pair is, because each one is lacking a bit. If I handed Al a one, he could reason that if the bit I can't see is also a one, then the parity of the original pair is even. But if the bit I can't see is a zero, then the parity of the original pair is odd. Bob is in exactly the same boat.
Riddle one. Al is no more able to state the parity of the original bit pair than he was before he was given his bit and the same is true for Bob. That is, each one has 50% of the data, but neither one has received any information at all.
Suppose now that I have 100 lab assistants, and 100 randomly generated bits of data. To assistant 1, I give all the bits except bit 1; to assistant 2, I give all the bits except bit 2; and so on. Each assistant has received 99% of the data. Yet none of them is any more able to state the parity of the original 100-bit data set than before they received 99 of the bits.
Riddle two. Even though each assistant has received 99% of the data, none of them has received any information at all.
Riddle three. The information in the 100 data bits cannot be in the bits themselves.
For, which bit is it in? Not bit 1, since that bit was given to 99 assistants, and didn't provide them with any information. Not bit 2, for the same reason. In fact, it is clear that the information cannot be in any of the bits themselves. So, where is it? Riddle four. Suppose my 100 bits have odd parity (say, 45 ones and 55 zeros). I arrange them on a piece of paper, so they spell the word "odd." Have I added information? If so, where is it? (FIG. 6)
Riddle five. Where is the information in a multiply encrypted message, since it completely disappears when one bit is removed?

FIG. 6 Feature
sets vs. sets of features.
5.7 Seven Riddles about Meaning
Thinking of information as a vehicle for expressing meaning, we now consider the idea of "meaning" itself. The following questions might seem silly, but the issues they raise are the very things that make intelligent computing and data mining particularly difficult. Specifically, when an automated decision support system must infer the "meaning" of a collection of data values in order to correctly make a critical decision, "silly" issues of exactly this sort come up . . . and they must be addressed. We begin this in Section 2 by introducing the notion of a domain ontology, and continue it in Section 11 for intelligent systems (particularly those that perform multi-level fusion).
For our purposes, the most important question has to do with context: does meaning reside in things themselves, or is it merely the interpretation of an observer? This is an interesting question I have used (along with related questions in axiology) when I teach my Western Philosophy class. Here are some questions that touch on the connection between meaning and context:
Riddle one. If meaning must be known/remembered in order to exists/persist, does that imply that it is a form of information? Riddle two. In the late 18th century, many examples of Egyptian hieroglyphics were known, but no one could read them. Did they have meaning? Apparently not, since there were no "rememberers." In 1798, the French found the Rosetta Stone, and within the next 20 or so years, this "lost" language was recovered, and with it, the "meaning" of Egyptian hieroglyphics. So, was the meaning "in" the hieroglyphics, or was it "brought to" the hieroglyphics by its translators? Riddle three. If I write a computer program to generate random but intelligible stories (which I have done, by the way), and it writes a story to a text file, does this story have meaning before any person reads the file? Does it have meaning after a person reads the file? If it was meaningless before but meaningful afterwards, where did the meaning come from? Riddle four. Two cops read a suicide note, but interpret it in completely different ways. What does the note mean? Riddle five. Suppose I take a large number of tiny pictures of Abraham Lincoln and arrange them, such that they spell out the words "Born in 1809"; is additional meaning present? Riddle six. On his deathbed, Albert Einstein whispered his last words to the nurse caring for him. Unfortunately, he spoke them in German, which she did not under stand. Did those words mean anything? Are they now meaningless? Riddle seven. When I look at your family photo album, I don't recognize anyone, or understand any of the events depicted; they convey nothing to me but what they immediately depict. You look at the album, and many memories of people, places, and events are engendered; they convey much. So, where is the meaning? Is it in the pictures, or is it in the viewer? As we can see by considering the questions above, the meaning of a data set arises during an act of interpretation by a cognitive agent. At least some of it resides outside the data itself. This external content we normally regard as being in the domain ontology; it is part of the document context, and not the document itself.
6. Data Complexity
When talking about data complexity, the real issue at hand is the accessibility of latent information. Data are considered more complex when extracting information from them is more difficult.
Complexity arises in many ways, precisely because there are many ways that latent information can be obscured. For example, data can be complex because they are unwieldy. This can mean many records and/or many fields within a record (dimensions). Large data sets are difficult to manipulate, making their information content more difficult and time consuming to tap.
Data can also be complex because their information content is spread in some unknown way across multiple fields or records. Extracting information present in complicated bindings is a combinatorial search problem. Data can also be complex because the information they contain is not revealed by available tools. For example, visualization is an excellent information discovery tool, but most visualization tools do not sup port high-dimensional rendering.
Data can be complex because the patterns that contain interesting information occur rarely. Data can be complex because they just don't contain very much information at all. This is a particularly vexing problem because it is often difficult to deter mine whether the information is not visible, or just not present.
There is also the issue of whether latent information is actionable. If you are trying to construct a classifier, you want to characterize patterns that discriminate between classes. There might be plenty of information available, but little that helps with this specific task.
Sometimes the format of the data is a problem. This is certainly the case when those data that carry the needed information are collected/stored at a level of precision that obscures it (e.g., representing continuous data in discrete form).
Finally, there is the issue of data quality. Data of lesser quality might contain information, but at a low level of confidence. In this case, even information that is clearly present might have to be discounted as unreliable.
7. Computational Complexity
Computer scientists have formulated a principled definition of computational complexity. It treats the issue of how the amount of labor required to solve an instance of a problem is related to the size of the instance (FIG. 7).
For example, the amount of labor required to find the largest element in an arbitrary list of numbers is directly proportional to the length of the list. That is, finding the largest element in a list of 2,000 numbers requires twice as many computer operations as finding the largest element in a list of 1,000 numbers. This linear proportionality is represented by O(n), read "big of n," where n is the length of the list.
On the other hand, the worst-case amount of labor required to sort an arbitrary list is directly proportional to the square of the length of the list. This is because sorting requires that the list be rescanned for every unsorted element to determine whether it is the next smallest or largest in the list. Therefore, sorting an arbitrary list of 2,000 numbers items requires four times as many computer operations as sorting a list of 1,000 numbers. This quadratic proportionality is represented by O(n2) read "big of n squared," where n is the length of the list.

FIG. 8 Complexity hierarchy for various text processing problems.
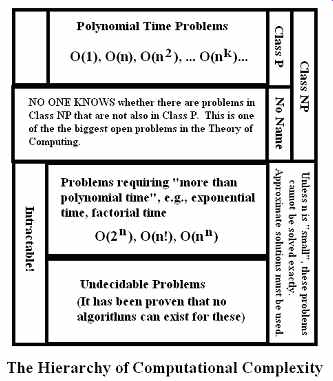
FIG. 7 The hierarchy of computational complexity.
Lots of research has been conducted to determine the Big complexity of various algorithms. It is generally held that algorithms having polynomial complexity, O(np), are tractable, while more demanding Big complexities are intractable. The details can't be addressed here, but we do note that many data mining problems (optimal feature selection, optimal training of a classifier, etc.) have a computational complexity that is beyond any polynomial level. In practice, this means that data miners must be content with solutions that are good enough. These are referred to as satisfying solutions.
Problems that are very computationally complex in their general case may fall into a class of problems referred to as NP-Hard. These problems, which have no known efficient algorithmic solutions, are frequently encountered in data mining work. Often problems in a domain are arranged in a hierarchy to help system architects make engineering trades (FIG. 8).
7.1 Some NP-Hard Problems
• The Knapsack Problem. Given cubes of various sizes and materials (and hence, values), find the highest value combination that fits within a given box.
• The Traveling Salesman Problem. Given a map with N points marked, find the shortest circuit (a route that ends where it starts) that visits each city exactly once.
• The Satisfiability Problem. Given a boolean expression, determine whether there is an assignment of the variables that makes it true.
• The Classifier Problem. Given a neural network topology and a training set, find the weights that give the best classification score.
7.2 Some Worst-Case Computational Complexities
• Determining whether a number is positive or negative: O(1) = constant time
• Finding an item in a sorted list using binary search: O(log(n))
• Finding the largest number in an unsorted list: O(n)
• Performing a Fast Fourier Transform: O(n*log(n))
• Sorting a randomly ordered list: O(n2)
• Computing the determinant of an n-by-n matrix: O(n3)
• Brute-force solution of Traveling Salesman Problem: O(n!)
8. Summary
The purpose of this section was to provide the reader with a grounding in the fundamental principles of data mining as a technical practice. Having read this section, you are now able to define data mining from both a philosophical and operational perspective, and enumerate the analytic functions data mining performs. You know the different types of data that arise in practice. You have been introduced to the basics of computational complexity theory, and the unavoidable presence of intractability.
Most importantly, you have considered the important differences between data and information.
Now that you have been introduced to some terminology and the fundamental principles of data mining, you are ready to continue with a summary overview of data mining as a principled process.
Coming next...
The next section presents a spiral methodology for managing the data mining process.
The key principles underlying this process are summarized in preparation for the detailed treatments that follow later.