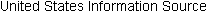The words output, unemployment, and inflation appear daily in newspapers and on the evening news. So when I used these words in Section 1, you knew roughly what we were talking about.
It is now time to define these words more precisely, and this is what we do in the first three sections of this section.
Section 1 looks at output.
Section 2 looks at the unemployment rate.
Section 3 looks at the inflation rate.
Section 4 introduces two important relations between these three variables: Okun's law and the Phillips curve.
Section 5 then introduces the three central concepts around which the guide is organized:
The short run: What happens to the economy from year to year
The medium run: What happens to the economy over a decade or so
The long run: What happens to the economy over a half century or longer
Building on these three concepts, Section 6 gives you a road map to the rest of the guide.
1. Aggregate Output
Economists studying economic activity in the nineteenth century or during the Great Depression had no measure of aggregate activity (aggregate is the word macroeconomists use for total) on which to rely. They had to put together bits and pieces of information, such as the shipments of iron ore, or sales at some department stores, to try to infer what was happening to the economy as a whole.
It was not until the end of World War II that national income and product ac counts (or national income accounts, for short) were put together. Measures of aggregate output have been published on a regular basis in the United States since October 1947. (You will find measures of aggregate output for earlier times, but these have been constructed retrospectively.) Like any accounting system, the national income accounts first define concepts and then construct measures corresponding to these concepts. You need only to look at statistics from countries that have not yet developed such accounts to realize that precision and consistency in such accounts are crucial. Without precision and consistency, numbers that should add up do not; trying to understand what is going on feels like trying to balance someone else's checkbook. I shall not burden you with the details of national income accounting here. But because you will occasionally need to know the definition of a variable and how variables relate to each other, Super-Section 1 at the end of the guide gives you the basic accounting framework used in the United States (and, with minor variations, in most other countries) today. You will find it useful whenever you want to look at economic data on your own.
GDP: Production and Income
The measure of aggregate output in the national income accounts is called the gross domestic product, or GDP, for short. To understand how GDP is constructed, it is best to work with a simple example. Consider an economy composed of just two firms:
Firm 1 produces steel, employing workers and using machines to produce the steel.
It sells the steel for $100 to Firm 2, which produces cars. Firm 1 pays its workers $80, leaving $20 in profit to the firm.
Firm 2 buys the steel and uses it, together with workers and machines, to produce cars. Revenues from car sales are $200. Of the $200, $100 goes to pay for steel and $70 goes to workers in the firm, leaving $30 in profit to the firm.
We can summarize this information in a table:
Steel Company (Firm 1) Car Company (Firm 2)
Revenues from sales $100 Revenues from sales $200
Expenses $80 Expenses $170
Wages $80 Wages $70
Steel purchases $100
Profit $20 Profit $30
How would you define aggregate output in this economy? As the sum of the values of all goods produced in the economy-the sum of $100 from the production of steel and $200 from the production of cars, so $300? Or as just the value of cars, which is equal to $200?
========
Two economists, Simon Kuznets, from Harvard University, and Richard Stone, from Cambridge University, received the Nobel Prize for their contributions to the development of the national income and product accounts-a gigantic intellectual and empirical achievement.
You may come across another term, gross national product, or GNP. There is a subtle difference between "domestic" and "national," and thus be tween GDP and GNP. We ex amine the distinction in Section 18 and in Super-Section 1 at the end of the guide. For now, ignore it.
In reality, not only workers and machines are required for steel production, but so are iron ore, electricity, and so on.
I ignore these to keep the ex ample simple.
An intermediate good is a good used in the production of another good. Some goods can be both final goods and intermediate goods. Potatoes sold directly to consumers are final goods. Potatoes used to produce potato chips are intermediate goods. Can you think of other examples?
========
Some thought suggests that the right answer must be $200. Why? Because steel is an intermediate good: It is used in the production of cars. Once we count the production of cars, we do not want to count the production of the goods that went into the production of these cars.
This motivates the first definition of GDP:
1. GDP Is the Value of the Final Goods and Services Produced in the Economy during a Given Period.
The important word here is final. We want to count only the production of final goods, not intermediate goods. Using our example, we can make this point in another way. Suppose the two firms merged, so that the sale of steel took place inside the new firm and was no longer recorded. The accounts of the new firm would be given by the following table:
Steel and Car Company
Revenues from sales $200
Expenses (wages) $150
Profit $50
All we would see would be one firm selling cars for $200, paying workers $80 + $70 = $150, and making $20 + $30 = $50 in profits. The $200 measure would remain unchanged-as it should. We do not want our measure of aggregate out put to depend on whether firms decide to merge or not.
This first definition gives us one way to construct GDP: by recording and adding up the production of all final goods-and this is indeed roughly the way actual GDP numbers are put together. But it also suggests a second way of thinking about and constructing GDP.
2. GDP Is the Sum of Value Added in the Economy during a Given Period.
The term value added means exactly what it suggests. The value added by a firm is defined as the value of its production minus the value of the intermediate goods used in production.
In our two-firms example, the steel company does not use intermediate goods. Its value added is simply equal to the value of the steel it produces, $100. The car company, however, uses steel as an intermediate good. Thus, the value added by the car company is equal to the value of the cars it produces minus the value of the steel it uses in production, $200 - $100 = $100. Total value added in the economy, or GDP, equals $100 + $100 = $200. (Note that aggregate value added would remain the same if the steel and car firms merged and became a single firm. In this case, we would not observe intermediate goods at all-because steel would be produced and then used to produce cars within the single firm-and the value added in the single firm would simply be equal to the value of cars, $200.)
This definition gives us a second way of thinking about GDP. Put together, the two definitions imply that the value of final goods and services-the first definition of GDP- can also be thought of as the sum of the value added by all the firms in the economy-the second definition of GDP.
So far, we have looked at GDP from the production side. The other way of looking at GDP is from the income side. Go back to our example and think about the revenues left to a firm after it has paid for its intermediate goods: Some of the revenues go to pay workers- this component is called labor income. The rest goes to the firm-that component is called capital income or profit income (the reason it is called capital income is that you can think of it as remuneration for the owners of the capital used in production).
Of the $100 of value added by the steel manufacturer, $80 goes to workers (labor income) and the remaining $20 goes to the firm (capital income). Of the $100 of value added by the car manufacturer, $70 goes to labor income and $30 to capital income. For the economy as a whole, labor income is equal to $150 1$80 + $702, capital income is equal to $50 1$20 + $302. Value added is equal to the sum of labor income and capital income is equal to $200 1$150 + $502.
This motivates the third definition of GDP.
3. GDP Is the Sum of Incomes in the Economy during a Given Period.
To summarize: You can think about aggregate output- GDP-in three different but equivalent ways.
From the production side: GDP equals the value of the final goods and services produced in the economy during a given period.
Also from the production side: GDP is the sum of value added in the economy during a given period.
From the income side: GDP is the sum of incomes in the economy during a given period.
Nominal and Real GDP
U.S. GDP was $17,400 billion in 2014, compared to $543 billion in 1960. Was U.S. out put really 32 times higher in 2014 than in 1960? Obviously not: Much of the increase reflected an increase in prices rather than an increase in quantities produced. This leads to the distinction between nominal GDP and real GDP.
Nominal GDP is the sum of the quantities of final goods produced times their current price. This definition makes clear that nominal GDP increases over time for two reasons:
First, the production of most goods increases over time.
Second, the price of most goods also increases over time.
If our goal is to measure production and its change over time, we need to eliminate the effect of increasing prices on our measure of GDP. That's why real GDP is constructed as the sum of the quantities of final goods times constant (rather than current) prices.
If the economy produced only one final good, say, a particular car model, constructing real GDP would be easy: We would use the price of the car in a given year and then use it to multiply the quantity of cars produced in each year. An example will help here.
Consider an economy that only produces cars-and to avoid issues we shall tackle later, assume the same model is produced every year. Suppose the number and the price of cars in three successive years are given by:
Nominal GDP, which is equal to the quantity of cars times their price, goes up from $200,000 in 2008 to $288,000 in 2009-a 44% increase-and from $288,000 in 2009 to $338,000 in 2010-a 16% increase.
Year Quantity of Cars Price of Cars Nominal GDP Real GDP (in 2009 dollars)
2008 10 $20,000 $200,000 $240,000
2009 12 $24,000 $288,000 $288,000
2010 13 $26,000 $338,000 $312,000
To construct real GDP, we need to multiply the number of cars in each year by a common price. Suppose we use the price of a car in 2009 as the common price. This approach gives us in effect real GDP in 2009 dollars.
Using this approach, real GDP in 2008 (in 2009 dollars) equals 10 cars * $24,000 per car = $240,000. Real GDP in 2009 (in 2009 dollars) equals 12 cars * $24,000 per car = $288,000, the same as nominal GDP in 2005. Real GDP in 2010 (in 2009 dollars) is equal to 13 * $24,000 = $312,000.
So real GDP goes up from $240,000 in 2008 to $288,000 in 2009--a 20% increase--and from $288,000 in 2009 to $312,000 in 2010-an 8% increase.
How different would our results have been if we had decided to construct real GDP using the price of a car in, say, 2010 rather than 2009? Obviously, the level of real GDP in each year would be different (because the prices are not the same in 2010 as in 2009); but its rate of change from year to year would be the same as shown.
Two lessons to remember:
i. GDP is the measure of aggregate output, which we can look at from the production side (aggregate production), or the income side (aggregate income); and ii. Aggregate production and aggregate income are always equal.
Warning! People often use nominal to denote small amounts.
Economists use nominal for variables expressed in current prices. And they surely do not refer to small amounts: The numbers typically run in the billions or trillions of dollars.
You may wonder why I chose these three particular years.
Explanation given when I look at the actual numbers for the United States.
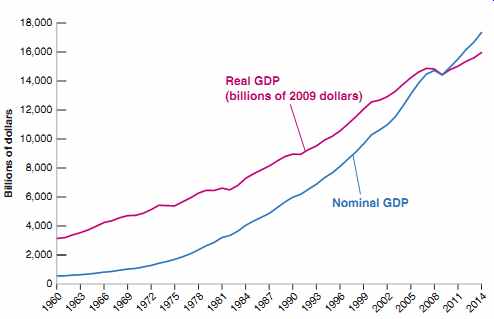
FIG. 1 Nominal and Real U.S. GDP, 1960-2014 From 1960 to 2014, nominal
GDP increased by a factor of 32. Real GDP increased by a factor of about
5. Source: Series GDPCA, GDPA: Federal Reserve Economic Data
To be sure, compute real GDP in 2010 dollars, and compute the rate of growth from 2008 to 2009, and from 2009 to 2010.
The year used to construct prices, at this point the year 2009, is called the base year.
The base year is changed from time to time, and by the time you read this guide, it may have changed again.
Suppose real GDP was measured in 2000 dollars rather than 2009 dollars. Where would the nominal GDP and real GDP lines on the graph intersect?
The problem when constructing real GDP in practice is that there is obviously more than one final good. Real GDP must be defined as a weighted average of the output of all final goods, and this brings us to what the weights should be.
The relative prices of the goods would appear to be the natural weights. If one good costs twice as much per unit as another, then that good should count for twice as much as the other in the construction of real output. But this raises the question: What if, as is typically the case, relative prices change over time? Should we choose the relative prices of a particular year as weights, or should we change the weights over time? More discussion of these issues, and of the way real GDP is constructed in the United States, is left to the Super-Section to this section. Here, what you should know is that the measure of real GDP in the U.S. national income accounts uses weights that reflect relative prices and which change over time. The measure is called real GDP in chained (2009) dollars. We use 2009 because, as in our example, at this point in time 2009 is the year when, by construction, real GDP is equal to nominal GDP. It is our best measure of the output of the U.S. economy, and its evolution shows how U.S. output has increased over time.
FIG. 1 plots the evolution of both nominal GDP and real GDP since 1960. By construction, the two are equal in 2009. The figure shows that real GDP in 2014 was about 5.1 times its level of 1960-a considerable increase, but clearly much less than the 32-fold increase in nominal GDP over the same period. The difference between the two results comes from the increase in prices over the period.
The terms nominal GDP and real GDP each have many synonyms, and you are likely to encounter them in your readings:
Nominal GDP is also called dollar GDP or GDP in current dollars.
Real GDP is also called: GDP in terms of goods, GDP in constant dollars, GDP adjusted for inflation, or GDP in chained (2009) dollars or GDP in 2009 dollars -if the year in which real GDP is set equal to nominal GDP is 2009, as is the case in the United States at this time.
In the sections that follow, unless I indicate otherwise, GDP will refer to real GDP and Yt will denote real GDP in year t.
Nominal GDP, and variables measured in current dollars, will be denoted by a dollar sign in front of them-for example, $Yt for nominal GDP in year t.
GDP: Level versus Growth Rate We have focused so far on the level of real GDP. This is an important number that gives the economic size of a country. A country with twice the GDP of another country is economically twice as big as the other country. Equally important is the level of real GDP per person, the ratio of real GDP to the population of the country. It gives us the aver age standard of living of the country.
In assessing the performance of the economy from year to year, economists focus, however, on the rate of growth of real GDP, often called just GDP growth. Periods of positive GDP growth are called expansions. Periods of negative GDP growth are called recessions.
The evolution of GDP growth in the United States since 1960 is given in FIG. 2.
GDP growth in year t is constructed as 1Yt - Yt - 12 / Yt - 1 and expressed as a percentage.
The figure shows how the U.S. economy has gone through a series of expansions, interrupted by short recessions. Again, you can see the effects of the recent crisis: zero growth in 2008, and a large negative growth rate in 2009.
Warning: One must be careful about how one does the
comparison: Recall the discussion in Section 1 about the standard of living in China.
This is discussed further in Section 10.
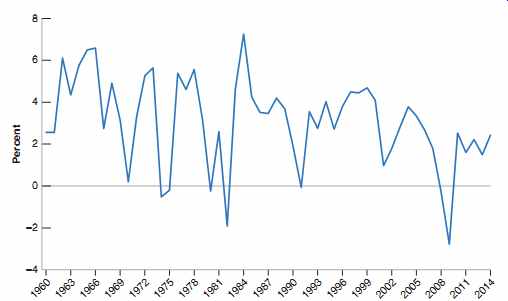
FIG. 2 Growth Rate of U.S. GDP, 1960-2014 Since 1960, the U.S. economy
has gone through a series of expansions, interrupted by short recessions.
The 2008- 2009 recession was the most severe recession in the period
from 1960 to 2014.
=============
Focus --- Real GDP, Technological Progress, and the Price of Computers
A tough problem in computing real GDP is how to deal with changes in quality of existing goods. One of the most difficult cases is computers. It would clearly be absurd to assume that a personal computer in 2015 is the same good as a personal computer produced, say 20 years ago: The 2015 version can clearly do much more than the 1995 version. But how much more? How do we measure it? How do we take into account the improvements in internal speed, the size of the random access memory (RAM) or of the hard disk, faster access to the Internet, and so on?
The approach used by economists to adjust for these improvements is to look at the market for computers and how it values computers with different characteristics in a given year. Example: Suppose the evidence from prices of different models on the market shows that people are willing to pay 10% more for a computer with a speed of 4 GHz (4,000 megahertz) rather than 3 GHz. The first edition of this guide, published in 1996, compared two computers, with speeds of 50 and 16 megahertz, respectively. This change is a good indication of technological progress. (A further indication of the complexity of technological progress is that, for the past few years, progress has not been made not so much by increasing the speed of processors, but rather by using multicore processors. We shall leave this aspect aside here, but people in charge of national income accounts cannot; they have to take this change into account as well.) Suppose new computers this year have a speed of 4 GHz compared to a speed of 3 GHz for new computers last year. And suppose the dollar price of new computers this year is the same as the dollar price of new computers last year. Then economists in charge of computing the adjusted price of computers will conclude that new computers are in fact 10% cheaper than last year.
This approach, which treats goods as providing a collection of characteristics-for computers, speed, memory, and so on-each with an implicit price, is called hedonic pricing ("hedone" means "pleasure" in Greek). It is used by the Department of Commerce-which constructs real GDP-to estimate changes in the price of complex and fast changing goods, such as automobiles and computers. Using this approach, the Department of Commerce estimates for example, that, for a given price, the quality of new laptops has increased on average by 18% a year since 1995. Put another way, a typical laptop in 2015 delivers 1.1821 = 32 times the computing services a typical laptop delivered in 1995. (Interestingly, in light of the discussion of slowing U.S. productivity growth in Section 1, the rate of improvement of quality has decreased substantially in the recent past, down closer to 10%.)
Not only do laptops deliver more services, they have become cheaper as well: Their dollar price has declined by about 7% a year since 1995. Putting this together with the information in the previous paragraph, this implies that their quality-adjusted price has fallen at an average rate of 18% + 7% = 25% per year. Put another way, a dollar spent on a laptop today buys 1.2521 = 108 times more computing services than a dollar spent on a laptop in 1995.
=============
2. The Unemployment Rate
Because it is a measure of aggregate activity, GDP is obviously the most important macroeconomic variable. But two other variables, unemployment and inflation, tell us about other important aspects of how an economy is performing. This section focuses on the unemployment rate.
We start with two definitions: Employment is the number of people who have a job.
Unemployment is the number of people who do not have a job but are looking for one.
The labor force is the sum of employment and unemployment:
L = N + U
labor force = employment + unemployment The unemployment rate is the ratio of the number of people who are unemployed to the number of people in the labor force:
u = U L
unemployment rate = unemployment / labor force
Constructing the unemployment rate is less obvious than you might have thought.
The cartoon notwithstanding, determining whether somebody is employed is relatively straightforward. Determining whether somebody is unemployed is more difficult. Recall from the definition that, to be classified as unemployed, a person must meet two conditions: that he or she does not have a job, and he or she is looking for one; this second condition is harder to assess.
Until the 1940s in the United States, and until more recently in most other countries, the only available source of data on unemployment was the number of people registered at unemployment offices, and so only those workers who were registered in unemployment offices were counted as unemployed. This system led to a poor measure of unemployment. How many of those looking for jobs actually registered at the unemployment office varied both across countries and across time.
Those who had no incentive to register-for example, those who had exhausted their unemployment benefits-were unlikely to take the time to come to the unemployment office, so they were not counted. Countries with less generous benefit systems were likely to have fewer unemployed registering, and therefore smaller measured unemployment rates.
Today, most rich countries rely on large surveys of households to compute the un employment rate. In the United States, this survey is called the Current Population Survey (CPS). It relies on interviews of 60,000 households every month. The survey classifies a person as employed if he or she has a job at the time of the interview; it classifies a person as unemployed if he or she does not have a job and has been looking for a job in the last four weeks. Most other countries use a similar definition of unemployment. In the United States, estimates based on the CPS show that, in July 2015, an average of 148.9 million people were employed, and 8.3 million people were unemployed, so the unemployment rate was 8.3/(148.9 + 8.3) = 5.3%.
The 60,000 households are chosen as a representative sample of the whole U.S. population. Thus, the sample pro vides good estimates of what is happening for the population as a whole.
FIG. 3 U.S. Unemployment Rate, 1960-2014 Since 1960, the U.S. unemployment
rate has fluctuated between 3 and 10%, going down during expansions and
going up during recessions.
The effect of the recent crisis is highly visible, with the unemployment rate reaching close to 10% in 2010, the highest such rate since the early 1980s. Source: Organization for Economic Co-operation and Development, Unemployment Rate: Aged 15-64: All Persons for the United States© [LRUN64TTUSA156N], retrieved from FRED, Federal Reserve Bank of St. Louis.
During the crisis, as the U.S. unemployment rate in creased, the participation rate decreased from 66% to 63%. But, surprisingly, as unemployment has decreased, the participation rate has not re covered. Why this is so is not fully understood. One hypothesis is the recession was so deep that some workers, who lost their job, have permanently given up on trying to become employed.
Note that only those looking for a job are counted as unemployed; those who do not have a job and are not looking for one are counted as not in the labor force. When unemployment is high, some of the unemployed give up looking for a job and there fore are no longer counted as unemployed. These people are known as discouraged workers. Take an extreme example: If all workers without a job gave up looking for one, the unemployment rate would go to zero. This would make the unemployment rate a poor indicator of what is actually happening in the labor market. This example is too extreme; in practice, when the economy slows down, we typically observe both an increase in unemployment and an increase in the number of people who drop out of the labor force. Equivalently, a higher unemployment rate is typically associated with a lower participation rate, defined as the ratio of the labor force to the total population of working age.
FIG. 3 shows the evolution of unemployment in the United States since 1960. Since 1960, the U.S. unemployment rate has fluctuated between 3 and 10%, going up during recessions and down during expansions. Again, you can see the effect of the recent crisis, with the unemployment rate reaching a peak at nearly 10% in 2010, the highest such rate since the 1980s.
Why Do Economists Care about Unemployment?
Economists care about unemployment for two reasons. First, they care about un employment because of its direct effect on the welfare of the unemployed. Although unemployment benefits are more generous today than they were during the Great Depression, unemployment is still often associated with financial and psychological suffering. How much suffering depends on the nature of unemployment. One image of unemployment is that of a stagnant pool, of people remaining unemployed for long periods of time. In normal times, in the United States, this image is not right: Every month, many people become unemployed, and many of the unemployed find jobs. When unemployment increases, however, We're at 5.3% now, so not increasing the image be comes more accurate. Not only are more people unemployed, but also many of them are unemployed for a long time. For example, the mean duration of unemployment, which was 16 weeks on average during 2000-2007, increased to 40 weeks in 2011; it has de creased since, but at the time of writing, remains at a relatively high 30 weeks. In short, when the unemployment increases, not only does unemployment become both more widespread, but it also becomes more painful for those who are unemployed.
Second, economists also care about the unemployment rate because it provides a signal that the economy may not be using some of its resources. When unemployment is high, many workers who want to work do not find jobs; the economy is clearly not using its human resources efficiently. What about when unemployment is low? Can very low unemployment also be a problem? The answer is yes. Like an engine running at too high a speed, an economy in which unemployment is very low may be overusing its resources and run into labor shortages. How low is "too low"? This is a difficult question, a question we will take up at more length later in the guide. The question came up in 2000 in the United States. At the end of 2000, some economists worried that the unemployment rate, 4% at the time, was indeed too low. So, although they did not advocate triggering a recession, they favored lower (but positive) output growth for some time, so as to allow the unemployment rate to increase to a somewhat higher level. It turned out that they got more than they had asked for: a recession rather than a slowdown.
It is probably because of statements like this that economics is known as the "dismal science."
==========
Focus --- Unemployment and Happiness
How painful is unemployment? To answer the question, one needs information about particular individuals, and how their happiness varies as they become unemployed. This information is available from the German Socio-Economic Panel survey. The survey has followed about 11,000 house holds each year since 1984, asking each member of the household a number of questions about their employment status, their income, and their happiness. The specific question in the survey about happiness is the following: "How satisfied are you at present with your life as a whole?'', with the answer rated from 0 ("completely dissatisfied") to 10 ("completely satisfied").
The effect of unemployment on happiness defined in this way is shown in Figure 1. The figure plots the average life satisfaction for those individuals who were unemployed during one year, and employed in the four years before and in the four years after. Year 0 is the year of unemployment. Years -1 to -4 are the years before unemployment, years 1 to 4 the years after.
The figure suggests three conclusions. The first and main one is indeed that becoming unemployed leads to a large decrease in happiness. To give you a sense of scale, other studies suggest that this decrease in happiness is close to the decrease triggered by a divorce or a separation. The second is that happiness declines before the actual unemployment spell. This suggests that either workers know they are more likely to become unemployed, or that they like their job less and less. The third is that happiness does not fully recover even four years after the unemployment spell. This suggests that unemployment may do some permanent damage, either because of the experience of unemployment itself, or because the new job is not as satisfying as the old one.
In thinking about how to deal with unemployment, it is essential to understand the channels through which un employment decreases happiness. One important finding in this respect is that the decrease in happiness does not depend very much on the generosity of unemployment benefits.
In other words, unemployment affects happiness not so much through financial channels than through psychological channels. To cite George Akerlof, a Nobel Prize winner, "A person without a job loses not just his income but often the sense that he is fulfilling the duties expected of him as a human being."
The material in this box, and in particular the figure, comes in part from "Unemployment and happiness," by Rainer Winkelmann, IZA world of labor, 2014: 94, pp 1-9.
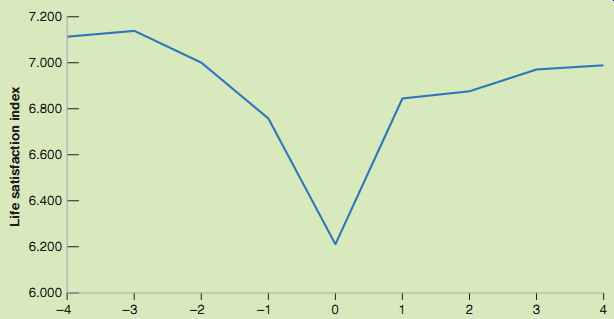
Figure 1 Effects of Unemployment on Happiness Source: Winkelmann 2014.
==========
Deflation is rare, but it happens. The United States experienced sustained deflation in the 1930s during the Great Depression (see the Focus Box in Section 9).
Japan has had deflation, off and on, since the late 1990s.
More recently, the Euro area has had short spells of deflation.
Index numbers are often set equal to 100 (in the base year) rather than to 1. If you look at the Economic Report of the President (see Section 1) you will see that the GDP deflator, reported in Table B3 is equal to 100 for 2009 (the base year), 102.5 in 2010, and so on.
Compute the GDP deflator and the associated rate of
inflation from 2008 to 2009 and from 2009 to 2010 in our car example in Section 1, when real GDP is constructed using the 2009 price of cars as the common price.
For a refresher for going from levels to rates of change, see Super-Section 2, Proposition 7.
3. The Inflation Rate
Inflation is a sustained rise in the general level of prices-the price level. The inflation rate is the rate at which the price level increases. (Symmetrically, deflation is a sustained decline in the price level. It corresponds to a negative inflation rate.) The practical issue is how to define the price level so the inflation rate can be measured. Macroeconomists typically look at two measures of the price level, at two price indexes: the GDP deflator and the Consumer Price Index.
The GDP Deflator
We saw how increases in nominal GDP can come either from an increase in real GDP, or from an increase in prices. Put another way, if we see nominal GDP increase faster than real GDP, the difference must come from an increase in prices.
This remark motivates the definition of the GDP deflator. The GDP deflator in year t, Pt, is defined as the ratio of nominal GDP to real GDP in year t:
Pt = Nominal GDPt Real GDPt = $ Yt Yt
Note that, in the year in which, by construction, real GDP is equal to nominal GDP (2009 at this point in the United States), this definition implies that the price level is equal to 1. This is worth emphasizing: The GDP deflator is called an index number. Its level is chosen arbitrarily-here it is equal to 1 in 2009-and has no economic interpretation. But its rate of change, 1Pt - Pt -12>Pt -1 (which we shall denote by pt in the rest of the guide), has a clear economic interpretation: It gives the rate at which the general level of prices increases over time-the rate of inflation.
One advantage to defining the price level as the GDP deflator is that it implies a simple relation between nominal GDP, real GDP, and the GDP deflator. To see this, reorganize the previous equation to get:
$Yt = PtYt
Nominal GDP is equal to the GDP deflator times real GDP. Or, putting it in terms of rates of change: The rate of growth of nominal GDP is equal to the rate of inflation plus the rate of growth of real GDP.
The Consumer Price Index
The GDP deflator gives the average price of output-the final goods produced in the economy. But consumers care about the average price of consumption-the goods they consume. The two prices need not be the same: The set of goods produced in the economy is not the same as the set of goods purchased by consumers, for two reasons:
Some of the goods in GDP are sold not to consumers but to firms (machine tools, for example), to the government, or to foreigners.
Some of the goods bought by consumers are not produced domestically but are imported from abroad.
To measure the average price of consumption, or, equivalently, the cost of living, macroeconomists look at another index, the Consumer Price Index, or CPI. The CPI has been in existence in the United States since 1917 and is published monthly (in contrast, numbers for GDP and the GDP deflator are only constructed and published quarterly).
The CPI gives the cost in dollars of a specific list of goods and services over time. The list, which is based on a detailed study of consumer spending, attempts to represent the consumption basket of a typical urban consumer and is updated every two years.
Each month, Bureau of Labor Statistics (BLS) employees visit stores to find out what has happened to the price of the goods on the list; prices are collected for 211 items in 38 cities. These prices are then used to construct the CPI.
Like the GDP deflator (the price level associated with aggregate output, GDP), the CPI is an index. It is set equal to 100 in the period chosen as the base period and so its level has no particular significance. The current base period is 1982 to 1984, so the average for the period 1982 to 1984 is equal to 100. In 2014, the CPI was 236.7; thus, it cost more than twice as much in dollars to purchase the same consumption basket than in 1982-1984.
You may wonder how the rate of inflation differs depending on whether the GDP deflator or the CPI is used to measure it. The answer is given in FIG. 4, which plots the two inflation rates since 1960 for the United States. The figure yields two conclusions:
The CPI and the GDP deflator move together most of the time. In most years, the two inflation rates differ by less than 1%.
But there are clear exceptions. In 1979 and 1980, the increase in the CPI was significantly larger than the increase in the GDP deflator. The reason is not hard to find. Recall that the GDP deflator is the price of goods produced in the United States, whereas the CPI is the price of goods consumed in the United States. That means when the price of imported goods increases relative to the price of goods produced in the United States, the CPI increases faster than the GDP deflator. This is precisely what happened in 1979 and 1980. The price of oil doubled. And although the United States is a producer of oil, it produces less than it consumes: It was and still is an oil importer. The result was a large increase in the CPI compared to the GDP deflator.
Do not ask why such a strange base period was chosen.
Nobody seems to remember.
Do not confuse the CPI with the PPI, or producer price index, which is an index of prices of domestically produced goods in manufacturing, mining, agriculture, fishing, forestry, and electric utility industries.
You may wonder why the effect of the 50% decrease in the price of oil in the second half of 2014 does not similarly show up as a larger decline of the CPI relative to the GDP deflator. The reason is that, although CPI inflation was indeed negative during the second half of 2014, this was offset by positive inflation in the first half of the year, and so does not show up in annual data.
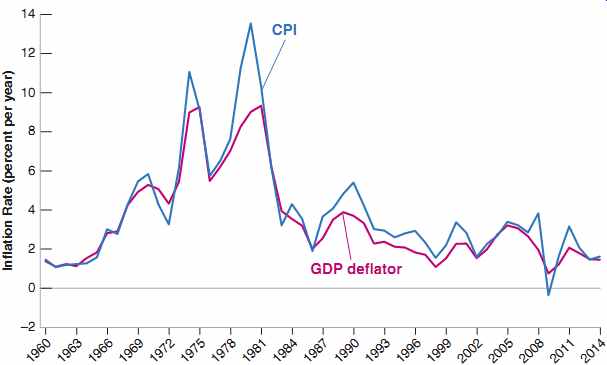
FIG. 4 Inflation Rate, Using the CPI and the GDP Deflator, 1960-2014
The inflation rates, computed using either the CPI or the GDP deflator,
are largely similar.
In what follows, we shall typically assume that the two indexes move together so we do not need to distinguish between them. We shall simply talk about the price level and denote it by Pt , without indicating whether we have the CPI or the GDP deflator in mind.
Why Do Economists Care about Inflation? If a higher inflation rate meant just a faster but proportional increase in all prices and wages-a case called pure inflation-inflation would be only a minor inconvenience because relative prices would be unaffected.
Take, for example, the workers' real wage-the wage measured in terms of goods rather than in dollars. In an economy with 10% inflation, prices would, by definition, increase by 10% a year. But wages in dollars would also increase by 10% a year, so real wages would be unaffected by inflation. Inflation would not be entirely irrelevant; people would have to keep track of the increase in prices and wages when making decisions. But this would be a small burden, hardly justifying making control of the inflation rate one of the major goals of macroeconomic policy.
So why do economists care about inflation? Precisely because there is no such thing as pure inflation:
During periods of inflation, not all prices and wages rise proportionately. Because they don't, inflation affects income distribution. For example, retirees in some countries receive payments that do not keep up with the price level, so they lose in relation to other groups when inflation is high. This is not the case in the United States, where Social Security benefits automatically rise with the CPI, protecting retirees from inflation. But during the very high inflation that took place in Russia in the 1990s, retirement pensions did not keep up with inflation, and many retirees were pushed to near starvation.
Inflation leads to other distortions. Variations in relative prices also lead to more uncertainty, making it harder for firms to make decisions about the future, such as investment decisions. Some prices, which are fixed by law or by regulation, lag behind the others, leading to changes in relative prices. Taxation interacts with inflation to create more distortions. If tax brackets are not adjusted for inflation, for example, people move into higher and higher tax brackets as their nominal income increases, even if their real income remains the same.
If inflation is so bad, does this imply that deflation (negative inflation) is good? The answer is no. First, high deflation (a large negative rate of inflation) would create many of the same problems as high inflation, from distortions to increased uncertainty. Second, as we shall see later in the guide, even a low rate of deflation limits the ability of monetary policy to affect output. So what is the "best" rate of inflation? Most macroeconomists believe that the best rate of inflation is a low and stable rate of inflation, somewhere between 1 and 4%.
4. Output, Unemployment, and the Inflation Rate: Okun's Law and the Phillips Curve
We have looked separately at the three main dimensions of aggregate economic activity: output growth, the unemployment rate, and the inflation rate. Clearly they are not independent, and much of this guide will be spent looking at the relations among them in detail. But it is useful to have a first look now.
This is known as bracket creep. In the United States, the tax brackets are adjusted automatically for inflation: If inflation is 5%, all tax brackets also go up by 5%-in other words, there is no bracket creep. By contrast, in Italy, where inflation averaged 17% a year in the second half of the 1970s, bracket creep led to a rise of almost 9 percentage points in the rate of income taxation. b
Newspapers sometimes con fuse deflation and recession.
They may happen together but they are not the same.
Deflation is a decrease in the price level. A recession is a decrease in real output.
We shall look at the pros and cons of different rates of inflation in Section 23.
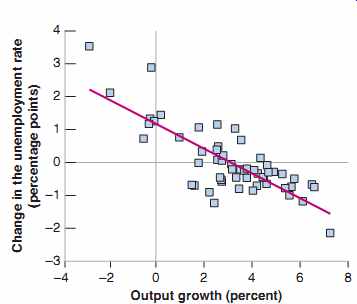
FIG. 5 Changes in the Unemployment Rate versus Growth in the United
States, 1960-2014 Output growth that is higher than usual is associated
with a reduction in the unemployment rate; output growth that is lower
than usual is associated with an increase in the unemployment rate.
Source: Series GDPCA,GDPA: Federal Reserve Economic Data (FRED)
research.stlouisfed.org/fred2.
In recent years, the growth rate at which the unemployment rate remains constant has been lower, around 2.5%. This reflects again the decrease in productivity growth (the rate of growth of output per worker), discussed in Section 1.
Arthur Okun was an adviser to President John F. Kennedy in the 1960s. Okun's law is, of course, not a law, but an empirical regularity.
Such a graph, plotting one variable against another, is called a scatterplot. The line is called a regression line.
For more on regressions, see Super-Section 3.
It should probably be known as the Phillips relation, but it is too late to change that.
top of page Article Index Home